Soal Terbimbing Untuk Pemahaman :
1. Sederhanakan bentuk-bentuk berikut :
a.7x + 3x
b.5a + 3b + a – 5b
c. (-3y2 + 2y – 4) + (2y2 – 3y + 5)
d. (2p3 + p – 5) – (2p2 + 3p – 4)
Penyelesaian :
a. 7x + 3x = ( .7. + .3. )x = ….
b. 5a + 3b + a – 5b = … + … + … + … = ( … + … )a + ( … – … )b = … ….
c. (-3y2 + 2y – 4) + (2y2 – 3y + 5) = … …. … … … …
= ( … ….)y2 + ( … …)y + ( … …)
= … …. …
d. (2p3 + p – 5) – (2p2 + 3p – 4) = … …. … … … …
= … …. ( … …)p + ( … …)
= … …. … …
2. Tentukan hasil perkalian berikut :
a. 5a x 2b
b. -3p x 4p
c.

d. 6ab2 x -2a3b x 4b2
Penyelesaian :
a. 5a x 2b = 5 x a x 2 x b = 5 x 2 x a x b = ….
b. -3p x 4p = … x … x … x … = … x … x … x … = ….
c.

= … x … x … x … x … x …
= … x … x … x … x … x … = …….
d. 6ab
2 x -2a
3b x 4b
2 = … x … x … x … x … x … x … x …
= … x … x … x … x … x … x … x …
= …. x … x ….
= ……
3. Jabarkan kemudian sederhanakan :
a. 3(2p – 3r)
b. 2(p – q) + 3p(p+q)
c. 3a(a – b) – 5(a2 – 2a + b)
4. Jabarkan dan sederhanakan :
a. (x – 3)(x + 1)
b. (2s + t)(3s – 5t)
c. (a2 + a)(3a + 2)
5. Jabarkan dan sederhanakan :
a. (2a + 1)2
b. (10b – 2)2
c. (-3n – 2m)2
Penyelesaian :
3. a. 3(2p – 3r) = 3x
2p +3x(-3r) = …. ….
b.

= … … … … = … … … … = … …
c. (-3n – 2m)2 = … … …. …. …. = … …. …. …. …..
= …. ….. …..
4. a. (x – 3)(x + 1) = … … … … … = … … …
b. (2s + t)(3s – 5t) = … … … … … = … … …
c. (a2 + a)(3a + 2) = … … … … … = … … …
5. a. (2a + 1)
2 = (2a + 1)(2a + 1) = … + … + … + … = … + … + …
b. (10b – 2)2 = (10b – 2)(10b – 2) = … + … + … + …
= … + … + …
c. (-3n – 2m)
2 = (-3n – 2m)(-3n – 2m) = … + … + … + …
= … + … + …
Soal Latihan 1 :
1. Sederhanakan :
a. a(a – b) – b (b – c) – c(c – a)
b. p2 + p – 3 – p(p – 2) + 2p(3p + 1)
2. Jabarkanlah :
a. (2x + 3)(3x – 2)
b. (2x2 – 5)(3x2 – x +2)
3. Jabarkanlah :
a. (3x + 2)2
b. (4p – ½)2
4. Jabarkan kemudian sederhanakan :
a. 2(x + 2)2 – (x + 1)2
b. -3ab(2a2 + 4ab – 5b2)
5. (3x + 2y)
2 – (2x – 5y)
2
2. Pembagian pada bentuk aljabar Selesaikan pembagian berikut :
a. 12ab : 3a
b. 16x2y3 : 12x3y
c.

Penyelesaian :
a. 12ab : 3a = (12 : 3) x (a : a) x b = ….. x …. x ….. = ……………….
b. 16x
2y
3 : 12x
3y =( …. : .…) x ( .… : .…) x ( .… : .…)
= ……. x ……… x ……… = …………..
c.

= ) : ……… = ( …. : ….) x ( …. : …. ) = …… x …… = ………..
Menentukan Faktor-faktor Bentuk Aljabar Memfaktorkan suatu bentuk aljabar artinya adalah mengubah bentuk penjumlahan/pengurangan suku-suku menjadi bentuk perkalian dari factor-faktornya. Perkalian bentuk aljabar terdiri dari 5 macam, yaitu :
1. Bentuk aljabar yang memiliki factor persekutuan, contoh : Faktorkanlah
bentuk :
a. 12x3 + 8x2 – 6x
b. 10a2b – 15a3b2 + 20a2b2
Penyelesaian :
a. 12x3 + 8x2 – 6x = 2.6.x.x.x + 2.4.x.x – 2.3.x
= 2x(6x2 + 4x – 3)
b. 10a2b – 15a3b2 + 20a2b2 = 5.2.a.a.b – 5.3.a.a.a.b.b + 5.a.a.b.b
= 5a2b (2 – 3ab + b)
2. Pemfaktoran bentuk a2 ± 2ab + b2
Rumus : a2 + 2ab + b2 = (a + b)2 a2 – 2ab + b2 = (a – b)2
contoh : Faktorkanlah :
a. 16x4 + 56x2y2 + 49y4
b. 36a2 – 60ab + 25b2
Penyelesaian
a. 16x4 + 56x2y2 + 49y2 = (4x2)2 + 2.(4x2).(7y2) + (7y2)2
= ( … + …)(… + …)
b. 36a2 – 60ab + 25b2 = ( … )2 – 2.( … ).( … ) + ( … )2
= ( … + …)(… + …)
3. Pemfaktoran bentuk selisih dua kuadrat
Rumus : a2 – b2 = (a + b)(a – b)
Contoh soal : Faktorkanlah :
a. y2 – 144
b. 9x2 – 64
c. 3a2 – 48
Penyelesaian :
a. y2 – 144 = (y)2 – (12)2 = (y + 12)(y – 12)
b. 9x2 – 64 = (3x)2 – (8)2 = ( … + … )( … – … )
c. 3a2 – 48 = 3(a2 – 16) = 3{( … )2 – ( … )2)
= 3( … + … )( … – … )
4. Pemfaktoran bentuk : x2 + bx + c , dimana b dan c bilangan real
Rumus : x2 + bx + c = (x + p)(x + q) dimana b = p + q dan c = p x q
Contoh soal :
Faktorkanlah :
a. m2 – 15m + 14
b. x2 + 16x – 36
c. X2 – 5xy – 24y2
Penyelesaian :
a. m2 – 15m + 14 = (m – 1)(m – 14)
b. x2 + 16x – 36 = (x + …)(x – …)
c. x2 – 5xy – 24y2 = (x + …)(x – …)
5. Pemfaktoran bentuk : ax2 + bx + c dimana a,b, dan c bilangan real & a ≠ 1
Cara penyelesaian : terlebih dahulu “ bx “ diuraikan menjadi dua suku dengan aturan : ax2 + bx + c = ax2 + rx + sx + c, dimana r dan s adalah dua bilangan dengan syarat jika dikali hasilnya = a x c dan jika dijumlah = b. r x s = a x c dan r + s = b
Contoh soal :
Faktorkanlah :
a. 5x2 + 13x + 6
b. 10p2 – 7p – 12
c. 8x2 – 26xy + 15y2
Penyelesaian :
a. 5x2 + 13x + 6 = 5x2 + 10x + 3x + 6
= 5x(x + 2) + 3(x + 2)
= (x + 2)(5x +3)
b. 10p2 – 7p – 12 = 10p2 + …. – …. – 12
= … ( … + … ) – … ( … + … )
= ( …. + …. )( …. – …. )
c. 8x2 – 26xy + 15y2 = 8x2 – …. – …. + 15y2
= … ( … – … ) – … ( … – … )
= ( …. – …. )( …. – …. )
Soal Latihan 2 :
Faktorkanlah selengkapnya :
1. 8p2q – 12pq2
2. 3abc + 6ab – 9bc
3. y4 – 16
4. 2x4 – 32
5. p4 – (2p – q)2
6. n2 – 14n + 24
7. x2 – 5px + 6p2
8. 2x2 + 7x + 6
9. 6y2 – y – 2
10. 2x2 – 5px + 3p
LATIHAN ULANGAN BAB 1
Pilihlah salah satu jawaban yang paling tepat!
1. Bentuk paling sederhana dari 5x + 3y – 2 – x + y + 2 adalah …
a. 4x + 3y c. 4x + 3y – 4
b. 4x + 4y d. 4x + 4y – 4
2. Jumlah dari 2p + 3q – 4 dan p – 3q + 2 adalah ..
a. 2p – 2 c. 2p – 6
b. 3p – 2 d. 3p – 6
3. Hasil pengurangan 6a2 – 12a dari 7a2 + 2a adalah …
a. –a2 – 14a c. a2 – 10a
b. –a2 – 10a d. a2 + 14a
4. Hasil dari (p – 3q)(2p – 5q) adalah …
a. 2p2 – 11pq – 15q2
b. 2p2 + 11pq – 15q2
c. 2p2 – pq – 15q2
d. 2p2 + pq – 15q2
5. (3x + 2y)(9x2 – 6xy + 4y2) = …
a. 27x3 + 8y3 .
b. 27x3 – 8y3 .
c. 27x3 + 24xy2 – 8y3 .
d. 27x3 – 36x2y – 8y3 .
6. Hasil dari (4p – 5q)2 adalah …
a. 16p2 – 20pq + 25q2
b. 16p2 – 20pq – 25q2
c. 16p2 – 40pq + 25q2
d. 16p2 – 40pq – 25q2
7. Hasil dari (–2a – )2 adalah …
a. 4a2 – 4 + 1/a2 c. 4a2 + 4 + 1/a2
b. 4a2 –4a + 1/a2 d. 4a2 – 4a + 1/a2
8. (2a + 3)2 – (a – 4)2 = …
a. 3a2 – 7 c. 3a2 + 4a + 25
b. 3a2 + 25 d. 3a2 + 20a – 7
9. Pemfaktoran dari 6x2y – 8xy2 adalah …
a. 2xy(3x – 4xy) c. 2xy(3x – 4y)
b. 2xy(3x – 6xy) d. 2xy(3x – 6y)
10. Pemfaktoran dari p(x + y) – q(x + y) adalah …
a. (x + y)(p + q) c. (x – y)(p + q)
b. (x + y)(p – q) d. (x – y)(p – q)
 ,
,  dan a, b, c,
dan a, b, c,



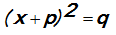 dengan q > 0
dengan q > 0 


 dengan
dengan 
 dan
dan 


 dan
dan  adalah akar-akar persamaan kuadrat
adalah akar-akar persamaan kuadrat  dengan
dengan 





 dan
dan 






